如果这篇博客帮助到你,可以请我喝一杯咖啡~
CC BY 4.0 (除特别声明或转载文章外)
一般来说,求解最短路问题时,我们面对的是有限节点的拓扑图,或者有最小精度的网格图,在这样的图上,可以应用 Dijkstra 或者 A* 。如果想要求连续平面地图上两点间的最短路,显然不能直接用上述算法求解,一个自然的想法是将连续地图进行离散化,然后在新的地图上求解。在这个过程中产生了许多新的问题:如何离散化?如何求解?如何优化路径?下面将一一分析并给出代码实现。
问题分析
连续地图离散化
对于欧几里得平面上的两个点,两点之间线段最短。但是如果是有障碍的平面地图,就不是那么好通过几何的方法求出最短路了,这时我们要可以尝试将连续地图进行离散化,转换为求解最短路问题时常见的拓扑图或者网格图。
正方形网格

正方形网格很容易生成和细分,寻路也非常简单,但有两个缺点:
- 两点间就算没有障碍,求出的路径也可能是分段的直线,需要进行路径优化
- 如果障碍不是规规整整的正方形网格中的点,例如图中的两个三角形,那么它们实际上会占据更多的面积,这会导致寻路产生偏差,这个误差可以随网格分辨率的提高而减小,但也会因此消耗更多的运算资源
对于不利用障碍本身,直接对地图进行网格细分的离散化方法,无论是正方形、三角网格或六边形网格,都会产生上述的误差。因此我们可以考虑利用地图和障碍的信息进行优化。
三角剖分
二维三角剖分可以将有边界的平面划分成若干三角形区域,经典算法有 Delaunay 三角剖分算法,鉴于三角剖分是几何学和计算机学的一个复杂问题,这里就不做进一步讨论和研究了,直接通过开源的 Triangle 库实现。
对示例地图进行三角剖分,效果如下
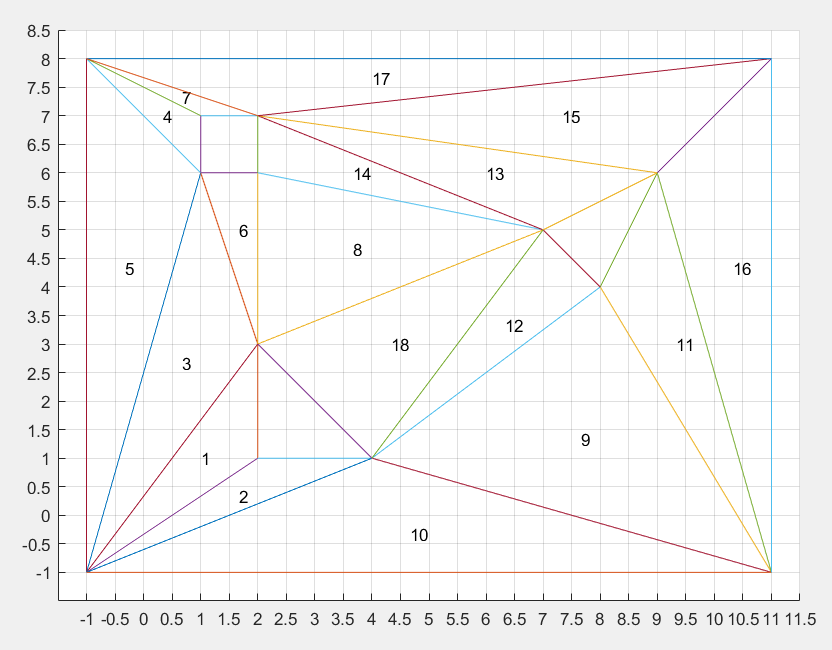
这样操作后,障碍物边界也成了三角网格的一部分,因此可以解决在障碍边界寻路不准确的问题。但三角网格同样有缺点,主要是寻路逻辑复杂,具体见后续分析。
寻路
无论是正方形网格还是三角网格,都具有鲜明的邻接关系,因此只要确定起始网格和终点网格,就能通过 Dijkstra 或者 A* 求出网格路径。然而在这里产生了一个非常重要的问题:寻路的距离怎么描述?
在正方形网格下,若以两个正方形中心距离定义两个正方形的距离,那么邻接的网格距离是固定的,可以为 $1$ 或者 $\sqrt{2}$ 。
然而在三角剖分得到的三角网格中,三角形的大小不一定相等,形状也不一致,如果用三角形中心的距离来描述,那么势必会产生较大的误差。例如上图三角形 5 的重心离左右顶点都很远, 3 和 5 的距离、 4 和 5 的距离哪一个大,就非常难对比,必须要说明起点和终点的位置。
拐角点法
为了精确计算距离,我们可以把寻路过程中经过的网格路径单独拿出来,在提取出的网格中计算起点到终点的距离,这里要用到一个网格寻路算法拐角点法(也有称漏斗算法,更为形象),这个算法在 GDC2006 上被提出,原 PPT 也不是很详细,这里简单介绍下算法步骤:
确定网格路径的邻接边
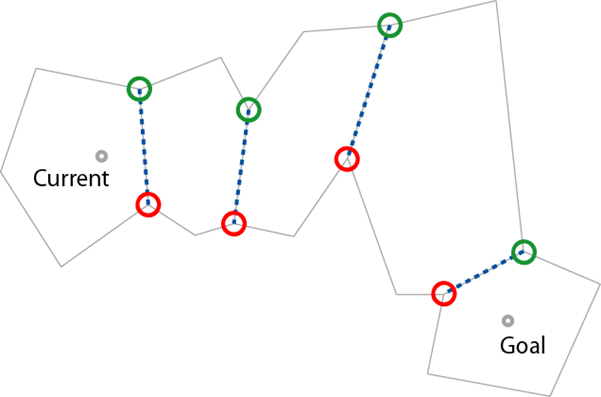
找到使“左邻接点-起点-右邻接点”夹角最小,且不改变夹角正负的左右两邻接点
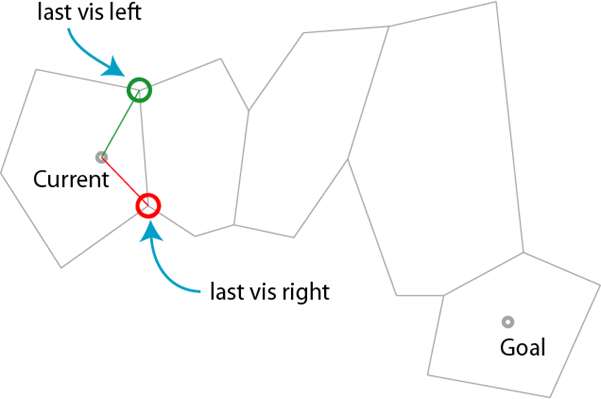
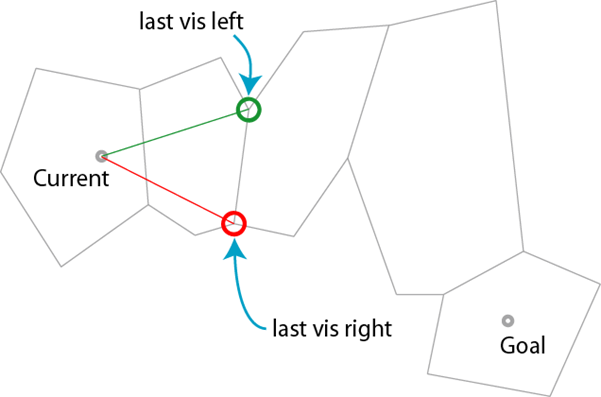
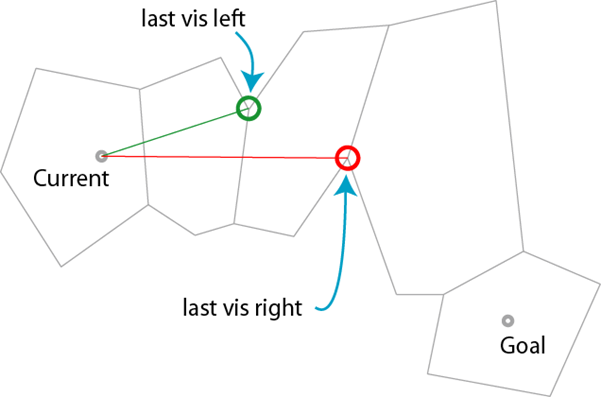
当夹角改变正负时,说明无法直接到达终点,需要拐弯,因此为路径添加拐点,并取拐点为新的起点,回到第 2 步继续算法,直到拐点为终点时,算法结束
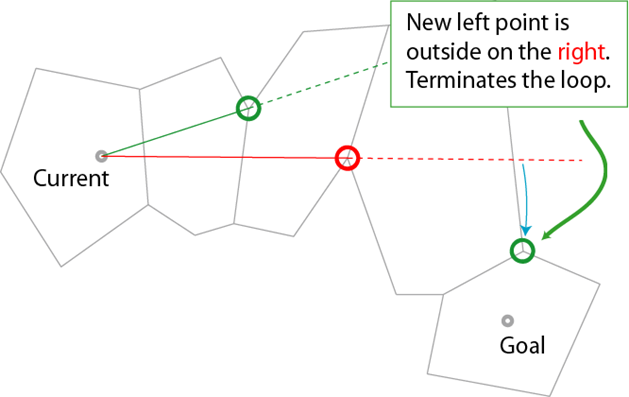
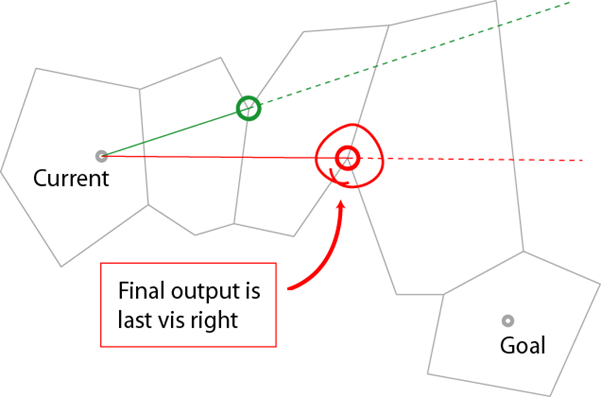
到这一步,我们可以求出三角网格上两点间的距离,已经可以通过“暴力搜索全部有效路径+计算路径长度”的方法在三角网格上求最短路了,这样的做法显然时间复杂度很高。但由于点到三角形的距离没有定义,因此对于中间路径仍然无法求解路径长度,因此无法应用 Dijkstra 算法。
A*算法
对于一般的拓扑图上最短路问题,只能通过 Dijkstra 、 SPFA 等算法求解。但是如果要搜索的图不是在拓扑空间上,而是定义在某个距离空间(又称度量空间,例如棋盘空间)或者范数空间(又称赋范空间,例如曼哈顿距离就是在1-范数空间上),那么就可以以两点间的距离作为启发式信息,估算当前点到终点的距离,从而始终选择“估算总路径长度=已走路径长度+剩余距离估计”最短的分支搜索,在保证算法正确性的同时,大大减少搜索树的大小。
假设要起点为 $(0,0)$ ,终点为 $(10,7)$ ,那么起点三角形是 1 ,终点三角形是 15 或者 16 ,可以取字典序小的三角形 15 。假设在寻路过程中,中间路径为三角形 1-3-6 ,那么起点、终点和中间路径如图
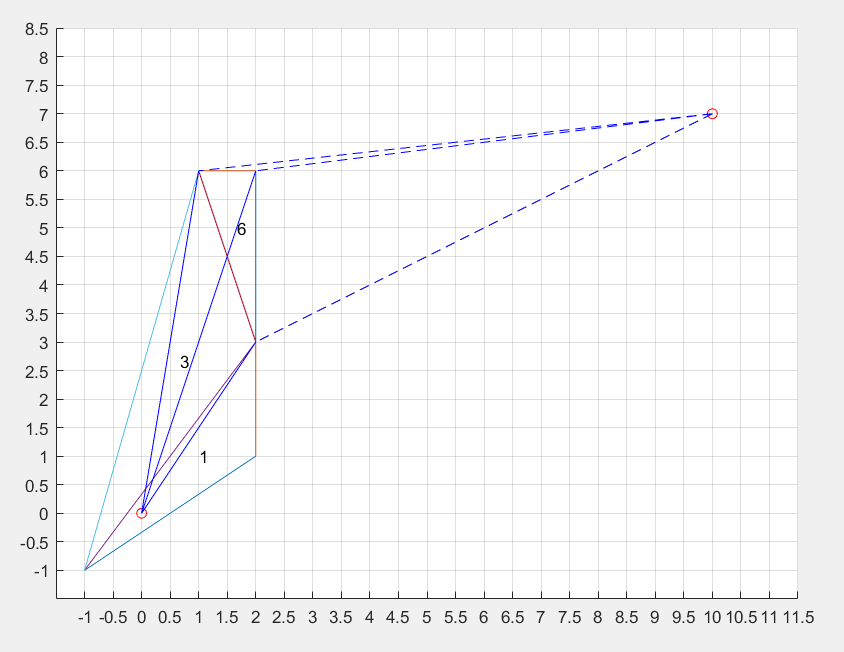
起点通过这段中间网格到达终点有三种可能的路径,分别经过三角形 6 的三个顶点。我们可以求出其中最短的那条,即经过 $(2,3)$ 的路径,然后用拐角点法求起点到 $(2,3)$ 的路径长度,即实路径(这里为单个线段)长度 $\sqrt{13}$ ,这个长度就可以定义为 Dijkstra 算法中的 dist[6] 。同时我们还得到了一个虚线段长度,即 $(2,3)$ 到终点的距离,这个距离可以作为 A* 的估价函数 h[6]。这样我们就保证了 f[6]=dist[6]+h[6] 最小,同时求出了三角形 6 到起点的距离和到终点的估价。
现在,我们在三角网络上按上述步骤跑一遍 A* ,就可以求出从起点到终点的最短路。
代码实现
懒得搬代码了,见 Triangulation-Based_Pathfinding ,文档里有简单的函数介绍和示例。如果有关于代码细节的疑问可以在评论区留言或者直接联系我。
